Решение теоремы Ферма.
уравнение
,
и
.
, что добавляет сомнений в том, что у него было доказательство общего случая.
, Дирихле и Лежандр в 1825 -- для
, Ламе -- для
.
при
может иметь лишь конечное число взаимно простых решений.
, а длины катетов через
и
:
- --
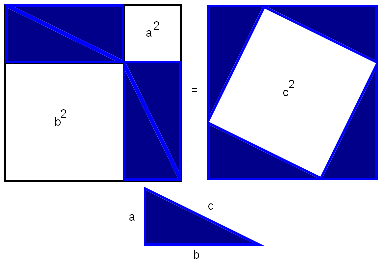
Расположим четыре равных прямоугольных треугольника так, как показано на рисунке 1.
- -- Четырёхугольник со сторонами c является квадратом, так как сумма двух острых углов 90®, а развёрнутый угол -- 180®.
- -- Площадь всей фигуры равна, с одной стороны, площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырёх треугольников и площади внутреннего квадрата.
- -- Четырёхугольник со сторонами c является квадратом, так как сумма двух острых углов 90®, а развёрнутый угол -- 180®.
VVVа
1