Хмельник Соломон Ицкович. Расчет линейных электрических цепей синусоидального тока

Хмельник С. И.

Расчет линейных электрических цепей синусоидального тока

Новый метод и MATLAB-программа

Аннотация

Предлагается новый метод и алгоритмы расчета линейных электрических цепей синусоидального тока.

Метод основан на недавно найденом вариационном принципе оптимума в линейных электрических цепях переменного тока. Это означает, что для любой такой цепи существует единственный оптимум некоторого функционала. Этот единственный оптимум может быть найден быстродействующим методом градиентного спуска, что очень привлекательно для приложений. При этом существует обратная зависимость между точностью и временем решения. На практике это означает, что пользователь может быстро перебирать приближенные варианты, а затем более точно расчитать выбранный вариант. Кроме того, вдвое сокращается количество уравнений задачи.

Приводятся открытые коды программ в системе MATLAB.

Содержание

Предисловие

1. Введение

2. Расчетные соотношения

3. Алгоритм расчета

4. Описание схемы

4.1. Ветви и узлы

4.2. Источники тока

4.3. Взаимоиндуктиности

5. Расчет схемы

6. Результаты расчета

7. Основная функция

4. Примеры расчета

Литература

Программы

Предисловие

Метод расчета основан на найденом автором вариационном принципе оптимума в линейных электрических цепях переменного тока [1]. Это означает, что для любой такой цепи существует единственный оптимум некоторого функционала. Этот единственный оптимум может быть найден быстродействующим методом градиентного спуска, что очень привлекательно для приложений. При этом существует обратная зависимость между точностью и временем решения. На практике это означает, что пользователь может быстро перебирать приближенные варианты, а затем более точно расчитать выбранный вариант.

На основе этого метода предлагается новый метод и алгоритмы расчета линейных электрических цепей синусоидального тока. Эти цепи могут иметь произвольную конфигурацию и содержать

-- сопротивления,

-- ёмкости,

-- индуктивнсти,

-- взаимоиндуктивности, в т.ч. с комплексными значениями,

-- источники напряжения,

-- источники тока.

Существующие методы расчета указанных электрических цепей основаны на их описании системой линейных уравнений и последующем решении этой системы. В нашем случае электрическая цепь перед расчетом преобразуется в т.н. безусловную электрическую цепь, параметры (напряжения и токи) которой с заданной точностью совпадают с одноименными параметрами исходной электрической цепи. Затем безусловная электрическая цепь расчитывается методом поиска оптимума некоторого функционала. При этом в отличие от изветных методов

-- существует обратная зависимость между точностью и временем решения; на практике это означает, что пользователь может быстро перебирать приближенные варианты, а затем более точно расчитать выбранный вариант;

-- вдвое сокращается количество уравнений задачи (точнее, система уравнений для обычной электрической цепи содержит уравнения первого и второго законов Кирхгофа, а для безусловной электрической цепи система уравнений содержит лишь уравнения второго закона Кирхгофа);

1. Введение

Рассмотрим электрическую цепь, пример которой приведен на фиг. 1, где

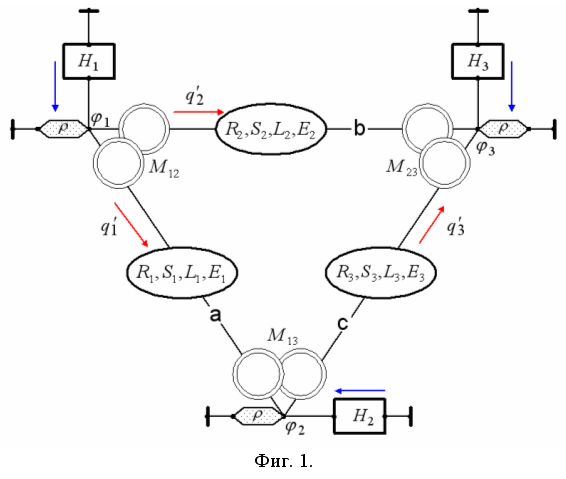
0x01 graphic

Методические сопротивления "ro" отсутствуют в реальной электрической цепи. Оно имеет смысл сопротивления, включенного между каждым узлом и общей точкой. Его включение позволяет преобразовать исходную электрическую цепь в т.н. безусловную электрическую цепь. Такая цепь описывается системой уравнений с меньшим числом неизвестных (исключаются уравнения первого закона Кирхгофа). Кроме того, функционал для безусловной электрической цепи имеет безусловный оптимум (что и дало незвание этой цепи). При большом "ro" безусловная электрическая цепь аппроксимирует обычную электрическую цепь с теми же параметрами (напряжениями и токами). Другими словами, режим безусловной электрической цепи при увеличении "ro". стремится к режиму аппроксимируемой электрической цепи Следовательно, расчет электрической цепи может быть заменен расчетом безусловной электрической цепи при достаточно больших "ro" Этот способ используется в дальнейшем.

2. Расчетные соотношения

3. Алгоритм расчета

Алгоритм расчета состоит в многократном решении системы уравнений (1) и заключается в следующем:

1. Преобразование схемы к стандартному виду - см. фиг. 1.

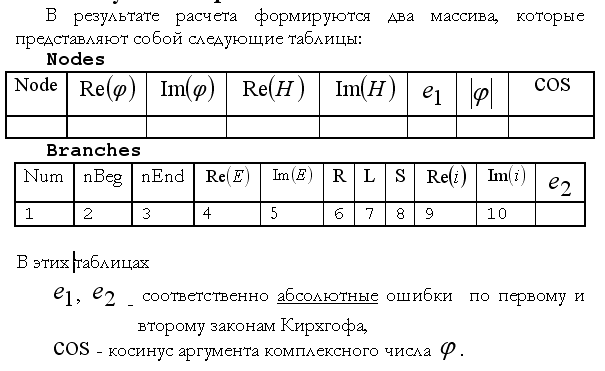
2. Подготовка таблиц описания исходной электрической схемы.

4. Описание схемы

Описание схемы представляет собой массивы B,H,M .

4.1. Ветви и узлы

Вначале узлы схемы нумеруются в произвольном порядке. Ветви схемы определяются номерами начального N1 и конечного N2 узла. Ветвь может содержать сопротивление R, источник напряжения U=Re(U)+j*Im(U), индуктивность L, конденсатор с обратной емкостью S. Выбор того, какой из двух узлов назначить начальным, имеет значение только в том случае, если ветвь содержит диод. Тогда начальным узлом назначается тот, который примыкает к положительному полюсу диода. Ток (определяемый в результате расчета) имеет положительное направление от начального к конечному узлу.

Каждая строка массива B описывает одну из ветвей и имеет следующий вид:

B(k,:)=[N1,N2,Re(U),Im(U),R,L,S]

4.2. Источники тока

Кроме того, схема может содержать источники тока, включенные между общей точкой и некоторыми узлами. Положительным направлением тока из источника является направление к узлу. Описание источников тока представляет собой массив следующего вида:

H=[H1,H2,...,HN,...]

где каждому узлу N ставится в соответствие число HN - комплексная величина тока источника тока или ноль, если в данном узле источника тока нет.

В реальной схеме источник тока включен в некоторую ветвь. Для приведения такой схемы к "каноническому" виду (описанному выше) необходимо проделать следующее:

-- выделить источник тока в отдельную ветвь (не содержащую других элементов),

-- преобразовать такую ветвь в два источника тока по схеме, приведенной на фиг. 2 - см. преобразование a--->b.

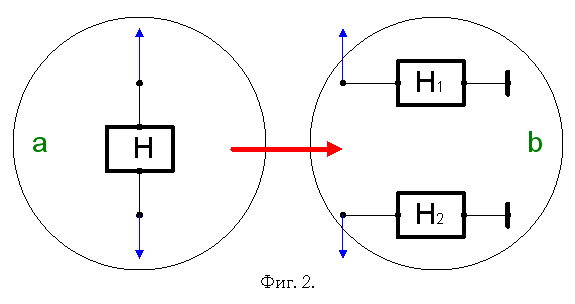
0x01 graphic

Очевидно, что каноническая схема должна удовлетворять условию

sum(Н)=0.

При постановке задачи необходимо следить за выполнением этого условия!

4.3. Взаимоиндуктиности

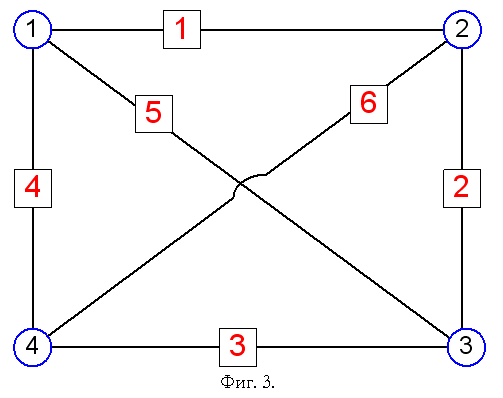
0x01 graphic

Аналогичные соотношения имеют место и для взимоиндуктивностей с неполным потокосцеплением. Из этих соотношений следует, что для реальных электрических цепей матрица M является положительно определенной [1]. Это свойство данной матрицы обеспечивает сходимость алгоритма.

В энергосистемах используются устройства, которые представляют собой трансформаторы с комплексным коэффициентом трансформации. Поэтому в программе предусмотрено, что матрица M может быть матрицей комплексных чисел.

5. Расчет схемы

Расчет схемы выполняется итеративно и результат расчета, как правило, является приближенным. При этом в результате появляются невязки - отклонения от нуля в уравнениях законов Кирхгофа. Им соответствуют относительные ошибки нарушения этих законов.

Количество итераций (т.е. длительность расчета) и достигнутые ошибки выполнения законов Кирхгофа регулируются

-- величиной коэффициента увеличения методического сопротивления и

-- величиной допустимой относительной ошибки второго закона Кирхгофа для безусловной схемы.

Эти величины задаются пользователем. Методическое сопротивление должно намного превышать все сопротивления ветвей для того, чтобы была достигнута допустимая ошибка первого закона Кирхгофа. Коэффициент увеличения методического сопротивления и является коэффициентом такого превышения. Допустимая относительная ошибка второго закона Кирхгофа для безусловной схемы должна намного превышать допустимую ошибку второго закона Кирхгофа для реальной схемы. По результатам пробного расчета пользователь должен корректировать указанные величины для получения желаемых значений относительных ошибок нарушения законов Кирхгофа.

6. Результаты расчета

0x01 graphic

7. Основная функция

М-функция для расчета электрической схемы имеет вид:

function [Branches,Nodes,erK2,erK1,k,ro] =...SinCir2 (kromin,eK2min,...

omega,maxIter,H,M,B)

Входными аргументами здесь являются

B - матрица, описанная в разделе 4.1,

M - матрица, описанная в разделе 4.3,

H - вектор, описанный в разделе 4.2,

eK2min - допустимое значение относительной ошибки второго закона Кирхгофа для безусловной схемы,

maxIter - допустимое число итераций,

kromin - коэффициент увеличения методического сопротивления,

omega - круговая частота.

Выходными величинами здесь являются

Branches - матрица, описанная в разделе 4.6,

Nodes - матрица, описанная в разделе 4.6,

erK2 - достигнутое значение относительной ошибки второго закона Кирхгофа,

erK1 - достигнутое значение относительной ошибки первого закона Кирхгофа,

k - выполненное количество итераций,

ro - используемое значение методического сопротивления.

8. Примеры расчета

Для примера приведена

function test4 ()

которая определяет входные параметры основной функции, обращается к ней и печатает ее выходные параметры. Этот тест расчитывает схему, изображенную на фиг. 3. Читатель может менять в этом тесте параметры обращения к основной функции.

Литература

1. Хмельник С.И. Вариационный принцип экстремума в электромеханических и электродинамических системах, третья редакция. Publisher by "MiC", printed in USA, Lulu Inc., ID 1769875, Израиль, 2010, ISBN 978-0-557-04837-3.

Оставить комментарий © Copyright Хмельник Соломон Ицкович Размещен: 07/02/2011, изменен: 21/06/2011. 16k. Статистика. Статья: Естествознание Электро... Иллюстрации/приложения: 8 шт.		Ваша оценка:
Аннотация: В книге [1] описан (в частности) метод расчета электрических цепей постоянного тока с диодами. Такую же книгу на английском можно скачать здесь, на СИ. В этой статье описывается программа для такого расчета в системе MATLAB. Данные для расчета подготавливаются в виде таблицы. Размерность задачи ограничена только ресурсами компьютера. Открытые коды этой MATLAB-программы можно приобрести у автора на сайте http://mic34.com/bookrumatlab.htm, позиция 362. С предложениями о дополнительных разработках можно обратиться по адресу solik@netvision.net.il.

Хмельник Соломон Ицкович : другие произведения.

Расчет линейных электрических цепей синусоидального тока